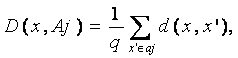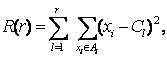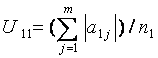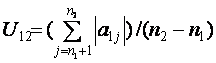4. МЕТОД КОРРЕЛЯЦИОННОЙ АДАПТОМЕТРИИ, ЕГО МОДИФИКАЦИИ, МОДЕЛИ АДАПТАЦИОННОГО СДВИГА, ОТСУТСТВИЕ ДОСТОВЕРНОЙ СВЯЗИ С КЛАСТЕРИЗАЦИЕЙ
4.1. Суть метода корреляционной адаптометрии
Для либиховских систем факторов
сравнение популяций по числу действующих факторов может служить полезным
средством для изучения адаптированности. Оказывается,
что корреляционные характеристики намного чувствительнее к адаптационному
напряжению, чем абсолютные величины параметров организмов. Основанный на этом
подход к изучению адаптации и его практическое применение к диспансеризации
человеческих популяций названы корреляционной адаптометрией.
Степень
скоррелированности физиологических параметров можно
оценить с помощью веса корреляционного графа, рассчитываемого как сумма весов
его ребер (сумма соответствующих коэффициентов корреляции):
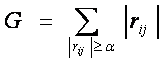 ,
,
где rij -
коэффициент корреляции между i-м и j-м параметрами, α определяется уровнем достоверности коэффициентов корреляции.
Можно
также использовать функциональные параметры спектра корреляционной матрицы.
Наиболее согласованно с качественно-физиологической картиной ведут себя
показатели:
f2 = ![]() li2; f3
= l1/lk; f6
=
li2; f3
= l1/lk; f6
= 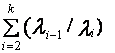 ,
,
где - l1³ l2³ …³ lk> lk+1= …=0
собственные числа корреляционной матрицы, α определяется уровнем
достоверности
Обрабатываемые
данные представляем в виде матрицы Z(n x m) такой, что zij
есть значение j-го
признака у i-го объекта
группы (каждый из n объектов представляется
вектором наблюдений из m признаков).
При
применении метода корреляционной адаптометрии для
каждой группы данных производятся следующие операции:
1.
Производится проверка гипотезы о нормальности закона распределения
выборки по критерию c2
2.
Стандартизуется матрица данных, для
чего переменные z заменяем на переменные x по
формулам:

где 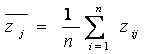 - среднее значение j-го признака;
- среднее значение j-го признака;
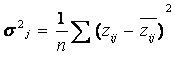 - дисперсия j-го признака.
- дисперсия j-го признака.
3.
Для всех показателей (признаков)
вычисляются парные коэффициенты ковариации и корреляции:
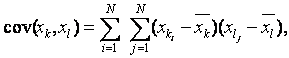
N - количество объектов в группе;
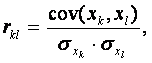
где
![]() - стандартное отклонение по xk,
- стандартное отклонение по xk,
![]() - стандартное отклонение по xl,
- стандартное отклонение по xl,
4.
Определяется достоверность
коэффициентов корреляции.
5.
Рассчитывается вес корреляционного
графа как сумма весов его ребер:
G=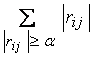 ,
,
где
rij
- коэффициент корреляции между i-м и j-м параметрами, a - число,
определяемое уровнем достоверности коэффициентов корреляции. Принимаются во
внимание только достоверные коэффициенты корреляции, значения которых больше
или равны a.
6.
Для определения статистической
достоверности при сравнении весов
корреляционного графа используются методы
бутстрепа
и «складного ножа» /83,262/.
С
помощью п.6 решается проблема интервального оценивания
веса корреляционного графа, когда стоит вопрос об оценке достоверности различий
групп объектов по степени скоррелированности набора показателей. В частности, выборки
бутстрепа генерируются следующим образом: по исходным
данным получают большое количество копий,
которые затем тщательно перемешиваются.
Далее, случайным образом формируются выборки такого же объема, как
исходная. По полученным выборкам подсчитываются
коэффициенты корреляции и для
них находятся стандартные статистические
характеристики, в частности,
доверительный интервал. Теоретические исследования /Пок49/ показали, что для коэффициентов корреляции ширина
интервала, соответствующего
распределению бутстрепа, и ширина
интервала, соответствующего реальному
распределению, как правило, совпадают.
Вероятность попадания значений веса корреляционного графа
случайной выборки из исследуемых групп
в доверительный интервал составляет 0,95.
Кроме
веса корреляционного графа, для оценки
взаимосвязи между физиологическими
показателями используются алгебраические параметры спектра корреляционной
матрицы. В /227/ показано, что элементы спектра являются устойчивыми
характеристиками и их взаимное расположение характеризует взаимосвязи во
множестве переменных. Спектр корреляционной
матрицы используется в основном в
практических применениях метода главных
компонент, в /75,79,83,213,231/ рассматриваются шесть функциональных параметров
f1 – f6 . В /83/ подробно изложена численная модель спектра корреляционной матрицы
и для оценки связей предлагаются также
шесть алгебраических параметров:
f1 = 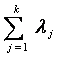 - сумма ненулевых собственных чисел; здесь и далее li – собственные числа корреляционной матрицы;
- сумма ненулевых собственных чисел; здесь и далее li – собственные числа корреляционной матрицы;
f2 = ![]() li2 – значение
избыточности системы признаков; чем больше этот показатель, тем сильнее степень
выраженности мультиколлинеарности.
li2 – значение
избыточности системы признаков; чем больше этот показатель, тем сильнее степень
выраженности мультиколлинеарности.
f3
= l1/lk – число
обусловленности корреляционной матрицы;
в вычислительной математике оно служит количественной мерой
независимости, если это число
близко к 1, то столбцы исходной матрицы данных линейно зависимы в сильной степени.
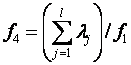 - доля первых l главных
компонент, где l равно числу доминирующих
элементов спектра.
- доля первых l главных
компонент, где l равно числу доминирующих
элементов спектра.
 - определитель корреляционной
матрицы.
- определитель корреляционной
матрицы.
f6 = 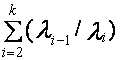 - суммарный показатель меры удаленности элементов спектра друг от друга.
- суммарный показатель меры удаленности элементов спектра друг от друга.
Рассмотрим
преимущества и недостатки веса корреляционного графа G и
алгебраических параметров спектра корреляционной матрицы.
Точность
оценки взаимосвязи между физиологическими показателями при помощи веса
корреляционного графа зависит от
точности оценок элементов корреляционной матрицы. Точность последней, в свою
очередь, зависит от качества выборки данных, и, в первую очередь, от количества
объектов в выборках. В то же время при
достаточно выраженной степени взаимосвязей в множестве
переменных спектр корреляционной матрицы является устойчивой статистикой, а
устойчивость собственных векторов, соответствующих элементам спектра, тем более
выражена, чем больше отличаются друг от
друга элементы спектра /227/. Однако из /213,227/ известно, что объем выборки,
необходимый для оценки l собственных
чисел ее корреляционной матрицы, должен в 2-3 раза превышать l независимо
от m. В настоящее время нет единого метода определения числа l и суммарной доли выделяемых
факторов f4.
Разработано более 20 способов
определения числа l в рамках трех подходов: алгебраического,
статистического и психометрического.
При
обработке медико-биологической информации мы очень часто сталкиваемся с
матрицами данных, имеющих пропуски, так как не всегда представляется возможным
зафиксировать все значения изучаемых показателей. При обработке таких массивов
данных применяют следующие подходы:
·
Если позволяет объем выборки, из
нее исключаются объекты, имеющие неполное описание.
·
Пропуски заполняются.
·
Стараются извлечь из имеющейся
выборки максимум информации без заполнения пропусков, используя при вычислении
коэффициентов корреляции каждую из имеющихся пар показателей.
Первый подход требует большого объема выборки. Второй, широко
распространенный подход обладает тем недостатком, что не всегда
удается автоматизировать процесс заполнения пропусков из-за сильной зависимости
показателей друг от друга, приходится формулировать критерий заполнения для
каждого показателя в отдельности. Третий подход используют в случае
уникальности обрабатываемого материала.
И физиологи, и медики
предпочитают третий подход, т.к. всегда считают с большим трудом полученные
данные уникальными, боятся потерять каждый объект наблюдений и считают
недопустимым искусственное введение показателей в их выборки, особенно если
речь идет о биохимических исследованиях крови, полученной из вены. Такие
данные действительно уникальны, т.к. при исследовании адаптационных процессов
проводится обследование здоровых по
существующим медицинским показаниям людей. А если это дети, да еще
новорожденные, результаты обследования становятся не просто уникальными, а
драгоценными.
При применении третьего метода при вычислении
коэффициентов корреляции с использованием каждой имеющейся пары значений
показателей часто получаем матрицу коэффициентов корреляции, не являющуюся
положительно определенной. Для таких матриц, естественно, невозможно рассчитать
собственные значения и, соответственно, алгебраические параметры спектра.
Итак,
подведем итоги. Если мы имеем полный набор данных у всех
объектов наблюдения оценку скоррелированности
физиологических параметров можно проводить и весом корреляционного
графа, и алгебраическими параметрами спектра корреляционной матрицы. В случае невозможности
расчета элементов спектра корреляционной матрицы оценку адаптационного
напряжения можно проводить только весом корреляционного графа G, а при
сравнительном анализе получать доверительные интервалы для G методом бутстрепа или складного ножа.
При
практическом использовании метода
корреляционной адаптометрии (см. примеры в главе 5) из алгебраических
параметров спектра наиболее наглядную разницу при сравнении дают f2 , f3 и f6. Наиболее
значимо различие групп прослеживается при сравнении по весу корреляционного
графа.
4.2. Математические модели сдвига параметров в результате
увеличения адаптационной нагрузки
4.2.1. Критерии согласования моделей с эмпирическими
данными.
Суть гипотетико-дедуктивного принципа,
лежащего в основе построения усложняющихся классов моделей, состоит в том, что
сначала создается гипотетическая конструкция, которая
дедуктивно развертывается, образуя целую
систему гипотез, а затем эта система подвергается опытной проверке, в ходе
которой она уточняется и конкретизируется. Дедуктивная система гипотез имеет
иерархическое строение. Прежде всего, в ней имеются гипотеза (гипотезы)
верхнего яруса и гипотезы нижних ярусов, которые являются следствием первых.
Каждый выход за рамки «более простой» гипотезы мотивируется противоречиями
между теорией и опытом. Эти противоречия и являются движущей силой развития
теории. Другой подход к моделированию, основывается на индуктивных обобщениях
научных фактов и в применении к проблеме формализации теории адаптации
представляется едва ли возможным, хотя бы ввиду почти полного отсутствия
фундаментальных научных разработок в этой области.
В данном разделе предпринимается
попытка построения последовательности
моделей адаптации, основанных на эффекте группового стресса. Из предложенных
моделей выбирается та, которая не противоречит эмпирическим данным.
Пусть
зафиксирован некоторый набор параметров. Множество возможных наборов значений
этих параметров естественно назвать пространством состояний (точнее,
пространством наблюдаемых проекций состояний). Каждый организм характеризуется
вектором значений параметров (точкой), а наблюдаемая группа – некоторым
конечным множеством («облаком») точек в этом пространстве. С ростом
адаптационной нагрузки увеличиваются
корреляции между параметрами и
растут дисперсии. При этом в начальном состоянии «лучшей
адаптированости» (с относительно низким уровнем скоррелированности физиологических параметров) все факторы
примерно равнозначны и размерность многообразия, вблизи которого расположено
облако точек, максимальна. Если реакция на возросшее адаптационное напряжение
определяется одним лимитирующим фактором, то следует ожидать, что множество
точек, соответствующее группе, окажется в окрестности одномерного многообразия
(кривой) и будет характеризоваться, по существу, одним числом – степенью скомпенсированности лимитирующего фактора. Если же есть два
в среднем равнозначных фактора, то вместо кривой будет двумерное многообразие
(поверхность). Величина изменения (сдвига) параметров определяется тем, что
изменились значения управляющих адаптацией параметров (нам неизвестных). Последние, в свою очередь, могут зависеть от
текущих значений физиологических параметров, наблюдаемых на практике.
Возникает вопрос: нельзя ли по двум состояниям с низкой и более высокой
степенью скоррелированности физиологических
параметров в группах объектов получить аналитическое выражение величины
адаптационного сдвига?
В принципе задача может быть решена средствами регрессионного анализа, но
сложность состоит в том, что для этого значения физиологических параметров до и
после увеличения адаптационной нагрузки должны относиться к одним и тем же
объектам. На практике зачастую приходится сравнивать однотипные, но различные
по составу выборки, поэтому для решения задачи можно воспользоваться только неиндивидуализированными
статистиками – в первую очередь, средними значениями, выборочными
ковариационными матрицами наблюдений и т.д.
Поскольку ковариационная матрица
получается при масштабировании
переменных с применением выборочных средних и дисперсий, то даже теоретически
инвариантные параметры могут меняться от выборки к выборке. Если выборки
различны и переменные измерены в неодинаковых единицах, удобно все переменные
привести к стандартному виду, используя для этого дисперсии, вычисленные по
совокупности выборок (выборочные средние берутся как обычно для каждой выборки
отдельно) /223/.
4.2.2. Модель независимых управляющих параметров
Ряд авторов /31,175/ придерживается
гипотезы о независимости в первом приближении добавки, определяющей вектор
сдвига параметров, от текущих значений физиологических параметров. Эта гипотеза
основывается на том факте, что прямой связи между ними нет: в границах нормы
одним и тем же значениям физиологических параметров могут соответствовать любые
значения управляющих параметров. Так например, при гипоксии
непосредственным патогенетическим
фактором, активизирующим комплекс приспособительных и
компенсаторных реакций организма является пониженное напряжение кислорода в
артериальной крови. При этом уменьшается насыщение гемоглобина кислородом и
общее его содержание в крови. Однако гемоглобин обладает свойством связывать
почти нормальное количество кислорода даже при значительном снижении парциального
давления кислорода в альвеолярном воздухе и в крови легочных сосудов: при рО2 100 мм рт. ст.
оксигемоглобин составляет 95-97%; при рО2 80 мм рт.
ст. соответственно 90%; при рО2 50 мм рт. ст. - 80% /2/. Таким образом, при двукратном уменьшении
парциального давления кислорода - параметра, регулирующего степень выраженности
адаптивных реакций - содержание оксигемоглобина варьирует незначительно.
Выясним, в
каких пределах гипотеза о
независимости управляющих параметров от текущих значений физиологических
показателей не будет противоречить неиндивидуализированным
статистическим данным. Пусть Х = {Х1, Х2,
..., Хn} - n - мерный вектор с составляющими Х1,
Х2, ..., Хn, которые
являются значениями физиологических параметров до адаптационной нагрузки; Y = (Y1, Y2,…Yn) - n-мерный случайный вектор значений физиологических параметров после
воздействия адаптационных факторов, когда увеличились корреляции между
параметрами и дисперсии; А - неизвестный n-мерный случайный вектор сдвига
значений параметров. Тогда
Y=X+A.
(4.1)
Условие независимости предполагает, что
случайный вектор А
не зависит от X.
Найдем из этих предположений, используя
(4.1), элемент ковариационной матрицы cov Y:
![]()
Отсюда,
учитывая условие независимости А от X,
![]() ,
или
,
или
![]() ,
(4.2)
,
(4.2)
где матрица covА является матрицей Грама и потому неотрицательно определена.
Тем самым, необходимым условием согласования гипотезы о статистической
независимости адаптационного сдвига от значений параметров с экспериментальными
данными является неотрицательная определенность разности ковариационных матриц ∆ = cov Y - covX.
Однако,
как показывает опыт (раздел 3.2), в спектрах матриц ∆ могут быть
отрицательные собственные числа, поэтому гипотеза о независимости в первом
приближении вектора адаптационного сдвига от значений физиологических
параметров не может быть безоговорочно принята.
4.2.3. Модель существенно одномерных сдвигов
В тех случаях, когда при адаптации
изменения в пространстве состояний происходят только в одном направлении и
∆ = covY - covX имеет ранг почти равный 1, можно
принять предположение, что адаптационный сдвиг параметров одномерен, т.е. имеет
вид ξb. Тогда Y=X + ξb, где ξ - постоянный вектор, причем,
║ξ║=1, b -
центрированная и нормированная случайная величина, может быть зависящая от X. Естественно предположить, что b линейно зависит от X: b = с + 1(Х), где ξ, - постоянный вектор, с - центрированная
и нормированная случайная величина, не зависящая от X (ее наличие объясняется тем, что
между Y и Х нет, как уже отмечалось, индивидуального соответствия), l(X) -линейная функция от Х. Таким образом,
Y=X+ ξ (c+l(X)).
(4.3)
Вид функции l(Х) практически невозможно восстановить, не
имея взаимно однозначного соответствия между точками облаков данных до
воздействия адаптационной нагрузки и после. Но можно вновь проверить, не
противоречат ли данные высказанному предположению. С учетом того, что в
евклидовом пространстве V линейная
функция 1(Х) представима в виде 1 (X) = (U, X), где U - некоторый вектор из V, можно записать: Yi = Xi + ξi (с+∑UkXk), тогда
(4.4)
![]()
![]()
Здесь ∆ij = (cov Y-cov X)ij; (cov X) U = q, откуда U = (cov X)-1q.
Поскольку в рассматриваемом случае
матрица ∆ = (cov Y - cov X) имеет ранг почти равный 1, то при
дополнительном условии, касающемся вектора q (q= аξ,
а - коэффициент пропорциональности), получим:
∆ij = ξi ξj {Dc+2a+a2((cov X )-1 ξ, ξ)}
= ξi ξjλ, (4.5)
где
Dc+2a+a2((cov X)- 1 ξ, ξ ) = λ (4.6)
λ - первое (максимальное по модулю)
собственное число матрицы ∆=соv Y - соv X; ξ - нормированный главный (соответствующий
максимальному по модулю собственному числу) собственный вектор матрицы ∆. Найдем оценку снизу для
(4.7)
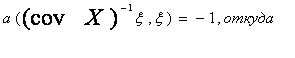
минимального значения λ, используя необходимое условие
экстремума:
![]()
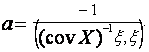
Т.к. в (4.6) коэффициент перед а2
положителен, то очевидно, что это будет минимальное значение а. При этом для оценки λmin снизу положим Dc=0 (Dc- положительная добавка):
![]()
Тем самым, необходимыми
условиями согласования модели существенно одномерных
сдвигов с экспериментом являются:
1. модуль наибольшего собственного числа матрицы ∆=соv Y - соv X много больше модулей всех остальных
собственных чисел этой матрицы;
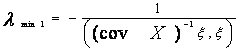
2. спектр матрицы ∆=соv Y - соv X лежит на прямой
справа от точки
Если
гипотеза не противоречит данным, то все полученные эмпирически значения
собственных чисел матрицы ∆=соv Y - соv X объяснимы в рамках построенной модели (λ1
≥ λmin1, i = 1, …n). В
этом случае (4.3) можно представить в виде:
Y = X+ ξ {c+a((cov X)-1 ξ ,X)}, (4.8)
где с - независимая от Х компонента управляющих параметров; а -коэффициент; ((cov X)-1 ξ ,X) - зависимая компонента, ξ - нормированный
главный (соответствующий
максимальному по модулю собственному числу) собственный вектор матрицы. ∆=соv Y - соv X.
Таким
образом, если эмпирические данные не дают оснований отвергнуть модель (4.8), то
можно считать, что в результате увеличения адаптационной нагрузки наблюдаемые
значения физиологических параметров сдвигаются в направлении главного
собственного вектора ξ
матрицы ∆=соv Y - соv X в зависимости от фактора U = ( cov Х)-1 ξ.
4.2.4.
Однофакторная модель
В общем
случае ранг матрицы ∆=соv Y - соv X может быть не равен 1, тогда положим
Y = X+A.+ ξ (l(X)), (4.9)
где А - независимый от Х случайный вектор; ξ - постоянный вектор произвольной
длины; l(Х) - линейная
функция от X. После аналогичных вышеприведенным преобразований получим для элемента матрицы ∆:
![]()
 (4.10)
(4.10)
Здесь ∆=(соv Y - соv X)ij; (covX)U=q, откуда U = (cov Х)-1q. Матрица ∆
симметрическая. Т.к. любое собственное число матрицы ∆ равно скалярному произведению (∆е, е), где е - некоторый вектор, удовлетворяющий условию ║e║ = 1, т.е. λ =(∆е, е), ║e║= 1 и имеют место неравенства: λmin ≤ λ ≤ λmax, где - λmin , λmax соответственно минимальное и
максимальное собственные числа этой матрицы, то для нахождения оценки снизу λmin2 для минимального собственного
числа матрицы ∆ положим А=0 (поскольку (М (АiAj) е, е) > 0). Тогда решаем
задачу:
(∆е, е) = λ =(ξ,, е)2 ((cov X)-1 q, q) + 2 (ξ,, е)(e, q)→min (4.11)
Для любого набора значений (ξ,, е) и (е, q) можно произвольно выбрать q (║q║=1). Пусть q - собственный
вектор положительно определенной симметрической матрицы (cov
X)-1, соответствующий ее
минимальному собственному числу λmin (Х*), т.е.
((cov X)-1 q, q) = λmin (Х*) = 1/ λmax (X),
(4.12)
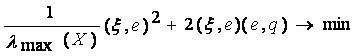
где λmax (X) > 0 - максимальное
собственное число матрицы covX (положительно
определенной симметрической). С учетом этого получим:
(4.13)
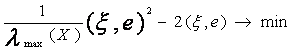
В силу независимости выбора положим е = - q и тогда задача сводится к
отысканию минимума функции по (ξ, е):
Отсюда значение аргумента, при котором достигается минимум
(4.11): (ξ ,е) = λmax (X). При этом оценка снизу для λmin будет
λmin2 = - λmax(X),
(4.14)
где - λmax(X ) - максимальное собственное число матрицы cov Y. Для этого случая
Y =Х+А+ ξ ((covX)-1q,X), (4.15)
где ξ - некоторый постоянный вектор; q - собственный вектор матрицы (cov X)-1, соответствующий ее минимальному
собственному числу; А - независимая
от значений Х физиологических
показателей компонента управляющих параметров; ((covX)-1q,X) -
зависимая от Х компонента.
Т.е.,
если принять модель (4.15), то следует предположить, что при усилении
адаптационной нагрузки (и повышении корреляций) физиологические параметры
сдвигаются в направлении, определяемом суммой двух векторов: случайного
вектора, не зависящего от текущих значений физиологических параметров, и
некоторого постоянного неизвестного вектора ξ. Фактором, в зависимости от которого этот сдвиг происходит, будет
фактор U = (cavX)-1q (q - собственный вектор матрицы (cov X)-1, соответствующий ее минимальному собственному числу).
Необходимым условием для согласования модели однофакторного сдвига
параметров будет равенство нижней оценки минимального собственного числа
матрицы ∆=соv Y - соv X и максимального
собственного числа матрицы cov X:
λmin2 = -
λmax(X).
Последняя модель, как свои частные предельные случаи,
содержит и модель независимых управляющих параметров, и модель существенно одномерных сдвигов. Первую - в тех случаях,
когда зависимостью сдвига от Х можно
пренебречь, вторую - когда ранг матрицы ∆=соv Y - соv
X
практически равен 1.
На практике было проверено, в каких
пределах - (4.7) или (4.14) лежат эмпирические данные (используя критерии
согласования (4.8) и (4.15)), и можно ли ограничиться более узкой моделью.
4.2.5.
Анализ применимости различных моделей адаптационного сдвига в практических
исследованиях.
Для анализа применимости моделей в
практических исследованиях были использованы предоставленные сотрудниками
Российского Университета Дружбы Народов данные по адаптации к
гипоксии-гиперкапнии на 2-ой, 3-ей, 4-ой стадиях нагрузки студентов -иностранцев, прибывших из Латинской Америки (24 чел.) и
Юго-Восточной Азии (28 чел.). Показатели гемодинамики и газообмена в этих
группах снимались на 3-5 день после приезда студентов в Москву. Сформированная
нами смешанная группа (Юго-Восточная Азия + Латинская Америка, 34 чел.)
представляет аналогичные показатели для тех же стадий нагрузки, снятые после
нескольких месяцев проживания в Москве.
При этом были взяты показатели
частоты сердечных сокращений (ЧСС), ударного объема (УО), общего
периферического сопротивления (ОПС),
артериального давления систолического (АДс) и диастолического
(АДд), максимального объема дыхания (МОД),
потребления кислорода (О2), количества
выдыхаемого углекислого газа (СО2). Данные использовались для
представления таблицы 4.1.
Использовались также данные, предоставленные сотрудниками
Института медицинских проблем Севера РАМН, по состоянию липидного обмена плазмы
крови у детей пришлого населения Таймыра с нормальным весом и различной
степенью конституционально-экзогенного ожирения на 2-й (45 чел.) и 3-ей (49
чел.) стадиях глюкозотолерантной нагрузки. Для
корреляционного анализа нами были отобраны 8 показателей липидного спектра:
свободный холестерин (СХ), свободные жирные кислоты (СЖК), триглицериды
(ТГ), эфиры холестерина (ЭХС), лизофосфатидитхолин
(ЛФХ), сфингомиелин + фосфатидилсерин (СМ+ФС), фосфатидилхолин (ФХ), фосфатидилэтано.тамин (ФЭА). Результаты последующей обработки этих
данных показаны в первой строке таблицы 4.2.
Для
каждой из указанных групп на каждой стадии нагрузки находилась матрица парных
коэффициентов корреляции и по ней оценивалась
степень скоррелированности параметров
- вес корреляционного графа G).
Кроме того, анализировались данные,
предоставленные Институтом медицинских проблем Севера СО РАМН по
состоянию липидного обмена в эритроцитарных мембранах
здоровых нерожденных детей пришлого населения
Крайнего Севера 1-х, 2-х, 3-х, 4-х суток жизни (соответственно 19, 19, 20 и 18
чел.) и новорожденных средних широт Сибири
1-х, 3-х, 5-х суток жизни (соответственно 10,
17 и 14
чел.).
Для оценки степени скоррелированности
показателей в каждой группе по методу корреляционной адаптометрии
учитывались показатели: свободный холестерин (СХ), свободные жирные кислоты
(СЖК), триглицериды (ТГ), эфиры холестерина (ЭХС); лизолецитин (ЛЛ); сфингомиелин
(СМ), фосфатидилхолин (ФХ), фосфатидилэтаноламин
(ФЭА). Эти данные легли в основу результатов, представленных во 2-7 строках
таблицы 4.2.
Последние (8-я и 9-я) строки
таблицы 4.2 получены на основании данных, взятых из материалов Института медицинских
проблем Севера РАМЫ по состоянию ферментной активности в лимфоцитах и кислой
фосфатазы в нейгрофилах у здоровых новорожденных
детей пришлого населения г. Якутска 1-х (30 чел.), 3-х (28 чел.), 5-х (26 чел.)
суток жизни (осенний период года). Анализ скоррелированности
проводился на следующей системе показателей: содержание сукцинатдегидрогеназы
(СДГ), α-глицерофосфадегидрогеназы (α-ГФДГ), моноаминоксидазы (МАО), лактатдегидрогеназы
(ЛДГ), анаэробной фракции фермента ЛДГ (Н-ЛДГ), НАДФН2-дегидрогеназы (НАДФН),
кислой фосфатазы в шмфоцитах (КФл),
кислой фосфатазы (КФн) в нейтрофилах.
Исходными
данными для заполнения таблицы 4.3 послужили данные о ферментном составе лимфоцитарных мембран здоровых новорожденных детей пришлого
населения г. Якутск и Норильск (зима) 1-х (23 чел.), 3-х (13 чел.), 5-х (11
чел.) суток жизни. Анализировались показатели: содержание сукцинатдегидрогеназы
(СДГ), α-глицерофосфадегидрогеназы (α-ГФДГ), моноаминоксидазы (МАО), лактатдегидрогеназы
(ЛДГ), анаэробной фракции фермента ЛДГ (Н-ЛДГ), кислой фосфатазы (КФл).
По
содержанию фракций нейтральных липидов (фосфолипидов
- ФЛ, свободного холестерина - СХ, свободных жирных кислот -СЖК,
григлицеридов - ТГ, эфиров холестерина - ЭХС) в эритроцитарных мембранах здоровых порожденных детей пришлого
населения Крайнего Севера 1-х, 2-х, 3-х, 4-х суток жизни (21 чел., 19 чел., 21
чел., 18 чел. -соответственно) оценивалась степень скоррелированности
параметров и после соответствующих вычислений заполнялась таблица 4.4. Для всех
групп данных проверялась гипотеза о нормальности закона распределения
генеральной совокупности по критерию c2.
Обработка данных производилась с помощью процедур пакетов STATGRAPHICS, PC MATLAB, Microsoft Excel для Windows 95.
Выборки X и Y (параметры
до и после адаптационной нагрузки) назначались с учетом возрастания степени скоррелированности (G) и дисперсий показателей.
Каждая из выборок центрировалась, затем нормировалась на совместную
σ (выборка
Х объединялась для этого с Y). После этого находились
ковариационные матрицы cov X, cov
Y, ∆ =соv
Y - соv X. Спектры матриц ∆, а также оценки λmin1 и λmin2 по
критериям согласования (4.7) и (4.14) представлены в таблицах 4.1-4.4.
Собственные числа расположены в порядке убывания абсолютных значений.
Таблица 4.1
Собственные числа матриц ∆ и критериев
согласования λmin1 и λmin2
|
№ |
λ1 |
λ2 |
λ 3 |
λ 4 |
λ 5 |
λ 6 |
λ 7 |
λmin1 |
Λmin2 |
|
1 |
2.0482 |
1.1262 |
0.6997 |
-0.6714 |
0.2802 |
-0.1593 |
0.0135 |
-0.4019 |
-1.4639 |
|
2 |
2.6360 |
1.5910 |
0.6755 |
-0.6696 |
0.1464 |
-0.1100 |
0.0072 |
-0.3690 |
-1.3621 |
|
3 |
2.2386 |
1.1258 |
-0.8201 |
0.6157 |
-0.4285 |
0.0909 |
0.0134 |
-0.2041 |
-1.8181 |
|
4 |
2.2882 |
-1.1853 |
1.0447 |
-0.6949 |
0.3259 |
0.0642 |
-0.0348 |
-0.3540 |
-1.9657 |
|
5 |
-1.3736 |
0.7288 |
-0.5538 |
0.3431 |
-0.1227 |
0.0603 |
-0.0324 |
-0.9321 |
-2.9274 |
|
6 |
-1.2163 |
1.0214 |
0.6771 |
0.3942 |
-0.2562 |
0.2419 |
-0.0376 |
-1.6060 |
-2.2223 |
|
7 |
1.3712 |
0.9293 |
-0.5642 |
0.2827 |
-0.2122 |
-0.0677 |
0.0343 |
-0.3784 |
-1.8465 |
|
8 |
1.2798 |
-0.6152 |
0.6084 |
-0.2883 |
0.2429 |
-0.1494 |
-0.0811 |
-0.3666 |
-2.1379 |
Таблица 4.2
Собственные числа матриц ∆ и критериев
согласования λmin1 и λmin2
|
№ |
λ1 |
λ2 |
λ 3 |
λ 4 |
λ 5 |
λ 6 |
λ 7 |
λ 8 |
λmin1 |
Λmin2 |
|
1 |
2.5776 |
0.8996 |
-0.7272 |
0.3698 |
-0.3288 |
0.1016 |
-0.0559 |
-0.0218 |
-0.3501 |
-3.8310 |
|
2 |
3.9591 |
-1.1093 |
-0.7514 |
0.7077 |
-0.4696 |
0.1751 |
-0.1396 |
-0.0524 |
-0.2893 |
-2.7659 |
|
3 |
1.7595 |
-0.3250 |
0.9775 |
-0.8624 |
0.7678 |
-0.6693 |
0.3359 |
0.1253 |
-0.3619 |
-3.1613 |
|
4 |
3.1258 |
-2.5878 |
-1.5171 |
-0.5970 |
0.3445 |
-0.3134 |
0.2043 |
-0.0099 |
-0.2065 |
-3.7367 |
|
5 |
4.2705 |
-1.3027 |
0.7848 |
-0.7751 |
0.2659 |
-0.2184 |
0.0810 |
-0.0523 |
-0.1264 |
-3.2380 |
|
6 |
2.7249 |
-2.4238 |
1.0747 |
0.8933 |
0.7736 |
0.3469 |
-0.3274 |
0.0292 |
-0.0676 |
-2.8680 |
|
7 |
3.0016 |
2.0659 |
1.7502 |
-1.2210 |
0.7862 |
0.4288 |
-0.3515 |
0.1199 |
-0.3074 |
-1.9063 |
|
8 |
-1.5178 |
-1.4425 |
-0.9290 |
0.5992 |
0.3643 |
0.2123 |
-0.1877 |
0.0578 |
-1.5467 |
-2.5212 |
|
9 |
-2.6097 |
1.4740 |
-0.6958 |
0.4949 |
-0.4634 |
0.2508 |
-0.2181 |
-0.1187 |
-2.8274 |
-2.9893 |
Таблица 4.3.
Собственные числа матриц ∆ и критериев
согласования λmin1 и λmin2
|
№ |
λ1 |
λ2 |
λ 3 |
λ 4 |
λ 5 |
λ 6 |
λmin1 |
λmin2 |
|
1 |
3.1659 |
1.0485 |
-0.8129 |
0.3927 |
-0.2408 |
0.0153 |
-0.0672 |
-1.5802 |
|
2 |
-2.2412 |
1.7649 |
-0.8901 |
0.8155 |
0.4474 |
-0.1125 |
-2.2040 |
-2.6641 |
|
3 |
2.7095 |
1.7750 |
-0.9226 |
-0.7494 |
0.1125 |
0.0154 |
-0.0290 |
-1.8015 |
Таблица 4.4.
Собственные числа матриц ∆ и критериев
согласования λmin1 и λmin2
|
№ |
λ1 |
λ2 |
λ 3 |
λ 4 |
λ 5 |
λmin1 |
λmin2 |
|
1 |
2.9718 |
-0.8569 |
-0.2698 |
0.0843 |
-0.0192 |
-0.1662 |
-1.6729 |
|
2 |
1.6690 |
-0.7570 |
0.6401 |
0.1852 |
-0.1056 |
-0.7104 |
-1.6624 |
|
3 |
2.1265 |
1.7110 |
0.4695 |
0.1029 |
-0.0326 |
-05588 |
-1.1384 |
Анализ таблиц 4.1-4.4 показывает, что в спектрах всех
матриц есть отрицательные собственные значения. Поэтому гипотеза (4.1) о
независимости адаптационного сдвига от наблюдаемых значений физиологических
параметров на данных группах параметров не подтверждается.
При применении критерия
согласования (4.7) оказывается, что первые (максимальные по модулю) собственные
числа превышают непосредственно следующие за ними в среднем только в 2-3 раза и
спектры матриц ∆ лишь в нескольких случаях (две
последние строки таблицы 4.2) действительно лежат справа от найденной нижней
границы λmin1. В подавляющем большинстве случаев
этот критерий согласования не работает, и модель (4.8) не отвечает имеющимися эмпирическим данным.
Использование критерия (4.14),
напротив, показывает, что собственные числа всех анализируемых матриц больше lmin2. Следовательно, модель (4.15) не противоречит имеющимся данным и в
конкретной ситуации она может быть принята.
Таким образом, построена
последовательность усложняющихся моделей сдвига параметров при
адаптации. Анализ применимости моделей практических исследованиях показал,
что:
·
гипотеза о независимости
в первом приближении адаптационного сдвига от значений параметров противоречит
имеющимся эмпирическим данным;
·
простейшей, не противоречащей
данным является модель однофакторного сдвига параметров при усилении
адаптационной нагрузки.
4.3. Механизм повышения корреляций: отсутствие достоверной
связи с кластеризацией
При обсуждении эффекта группового
стресса и метода корреляционной адаптометрии часто
возникает вопрос о связи эффекта
повышения корреляций при адаптации с кластерообразованием.
В данном разделе дан краткий обзор методов и алгоритмов кластер-анализа.
К конкретным данным применены
алгоритмы ISODATA и иерархический
алгоритм «ближайшего соседа». Показано, что имеет место случай, когда облако
данных не делится на изолированные группы, а вытягивается в небольшом числе
направлений пространства состояний. Полученные результаты подтверждают
высказанное нами предположение об этом еще в 1987 г. / 59 /.
4.3.1. Обзор используемых методов и алгоритмов кластер-анализа
Из нужд медико-биологических, социально-экономических приложений
возникло огромное количество алгоритмов кластер-анализа,
приносящих успех при решении конкретных практических задач, но используемых
порой при отсутствии математических обоснований. Достаточно строгая теория, как
отмечается в /275/, охватывающая большую часть задач кластер-анализа,
была разработана под руководством Diday E.
Для проведения кластерного анализа
имеющихся данных в работе применены иерархический метод
«ближайшего соседа» и итеративный алгоритм ISODATA.
Принцип
работы иерархических агломеративных (дивизимных) процедур состоит в последовательном объединении
(разделении) групп элементов сначала самых близких (далеких), а затем все более
отдаленных (приближенных) друг от друга.
Иерархические процедуры дают достаточно
полный и тонкий анализ структуры исследуемого
множества наблюдений. Их привлекательной стороной является также
возможность наглядной интерпретации проведенного анализа.
Алгоритм "ближайшего соседа" и
его модификации описаны в /273,235,359,364/.
Агломеративный иерархический алгоритм
"ближайшего соседа" ("single
linkage or nearest neighbor
method") исходит из матрицы расстояний
между наблюдениями, в которой расстояние между
кластерами определяется по формуле:
![]() min
min
где Si -i-я группа или кластер; p-
расстояние; xi - i-е наблюдение.
На первом шаге алгоритма каждое наблюдение
Xi (i=1,2,...,n) рассматривается как отдельный кластер.
Далее на каждом шаге работы алгоритма происходит объединение двух самых близких
кластеров и по формуле (2.1) пересчитывается матрица расстояний, размерность
которой, естественно, снижается на единицу. Работа алгоритма заканчивается,
когда все исходные наблюдения объединены в один класс. Поскольку
расстояние между любыми двумя кластерами в этом алгоритме равно расстоянию
между двумя самыми близкими элементами, представляющими свои классы, то
получаемые в итоге кластеры могут иметь достаточно сложную форму, в частности'
они не обязаны быть выпуклыми; ведь два наблюдения попадают в один кластер,
если существует соединяющая их цепочка близких между собой элементов.
Это обстоятельство можно отнести как к достоинствам алгоритма, так и к его
недостаткам.
Для устранения опасности появления случайных, не характерных
для исследуемого явления объединений, предложена модификация алгоритма /364/.
Эта модификация состоит в том, что элементы исследуемой совокупности включаются
в рассмотрение в порядке убывания плотности наблюдений в их окрестности, причем
плотность оценивается как величина, обратная расстоянию до самого дальнего из т элементов, ближайших к данному. Целое
число т назначается заранее из
некоторых априорных соображений и, по смыслу использования в процедуре,
определяет число элементов (в количестве m+1) в кластере, являющемся
наиболее представительным, наиболее населенным из всех кластеров, образующихся
на первом шаге процедуры. Эти кластеры образуются по следующему правилу. Из
элементов исследуемой совокупности (Xi), занумерованных в порядке возрастания расстояния D, (т) от каждого из них до самого дальнего
из т ближайших к нему соседей,
выбираются вначале т точек, попавших
в окрестность точки Xs радиуса Ri(m), и из этих (k+1) точек формируется первый кластер Si. Затем
берется следующая по порядку точка Xi из числа п - m -1 оставшихся, т.е. не попавших в кластер Sl, и к ней
"притягиваются" для образования следующего класса все точки, из числа
не попавших в кластер Sl, попадающие в ее окрестность радиуса Ri2{m), и т.д. Следует отметить, что описанная модификация
алгоритма ближайшего соседа, оставаясь агломеративной
процедурой, уже не является, строго говоря, процедурой иерархической, так как
не предусматривает в качестве обязательного итога объединение всех наблюдений в
один класс.
Существуют и другие способы устранения
"цепочного эффекта" при образовании классов с помощью этого
алгоритма. Наиболее простым и естественным из них можно признать, например,
введение ограничения сверху на максимальное расстояние между элементами одного
класса: если при формировании классов для некоторых элементов получаемого
кластера взаимное расстояние превысит некоторый заданный порог, то эти элементы
следует разнести по какому-то дополнительному правилу в разные классы.
Известны также работы по применению иерархического кластерного анализа в задачах
классификации по неполным данным /364/ и на основе непараметрических критериев
/334/.
В отличие от иерархических методов,
которые требуют вычисления и хранения матрицы сходства между объектами порядка n x я, итеративные методы работают непосредственно с первичными данными.
Следовательно, они позволяют обрабатывать довольно большие маcсивы данных. Кроме того, алгоритмы, основанные на этих методах, делают
несколько просмотров данных и могут компенсировать последствия плохого
исходного разбиения. Большинство итерационных алгоритмов не допускают
перекрытия кластеров.
Поскольку характер параллельных процедур,
реализующихся с помощью итерационных алгоритмов, предусматривает одновременный
обсчет всех исходных наблюдений на каждом шаге алгоритма, то
очевидно, что полный перебор всех вариантов разбиения уже при числе
классифицируемых точек порядка нескольких десятков является практически
неосуществимым даже при заданном числе классов. Для того,
чтобы приблизиться к оптимальному разбиению набора данных, разработан широкий
круг эвристических итерационных алгоритмов /250,256,263 и др./. Но лишь малая
их часть имеет достаточное статистическое обоснование.
В /275/ предложен метод
автоматической классификации, при котором отыскивается разбиение исследуемого
множества объектов на классы, такие, что каждый объект больше похож на лучших представителей
своего класса, чем на представителей других классов. Понятие
"представители" класса или ядро класса имеет самый широкий смысл:
ядром класса может быть подгруппа точек из п элементов
(где п ³ 1), центр тяжести, ось, случайная переменная и т.д.. Задача состоит в
отыскании наилучших ядер, т.е. таких, которые наилучшим образом представляют
свои классы.
В самом общем виде
алгоритм классификации с помощью динамических ядер сводится к
следующему: каким-либо способом (эвристическим, случайным) выбирают k исходных
ядер. Затем производят группирование путем притягивания оставшихся
элементов: каждый из них присоединяют к
наиболее близко расположенному ядру.
Для полученного разделения по
определенному правилу вычисляют новые ядра и сравнивают новое разделение с
предыдущим. Если разделения и ядра остаются неизменными, то процесс прекращают,
а получившееся разделение на классы считают окончательным.
Метод
динамических ядер основан
на одновременном использовании
двух функций. Одна из них - функция присваивания (или функция назначения) - управляет
процессом присоединения элементов к ядру,
другая - функция
признаков (функция
представительства) - процессом выбора ядра на всех этапах, кроме
начального.
Пусть множество Е, состоящее из р элементов, должно быть
разделено на k классов. В каждом классе выбирают
представляющее его ядро, состоящее из q элементов. Множество ядер обозначим L = {A1, A2, ....
Ak}. Пусть Р = {P1, Р2, ..., Pk} - разделение
множества £ на k
классов. Назовем D (Аi,Рi) мерой рассогласования (несходства) ядра Аi с классом Рi (в отличие от этой групповой меры степень несходства между собой двух
отдельных элементов х
и у, где x, у Î Е, оценивается расстоянием d (x, у) между ними).
Критерием качества разбиения на классы
естественно считать минимум суммы:
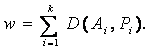
Пусть х - элемент множества Е.
При фиксированном наборе ядер [A1, A2 .... Ak} получаемое разделение определяется
функцией присваивания:
![]() где
где
![]()
На очередном шаге итерации
применяют функцию признаков таким образом, чтобы
получить новые ядра. При заданных Р = {Р1, Р2, ..., Рk} ищется L = {
A1, A2, ..., Ak}: Ai= {х
Î W /х Î группе из q элементов,
которые минимизируют D(x,Pi )}.
Здесь W - множество
признаков. Функция g(P) такова, что g(P) =L. Процесс
классификации состоит в итеративном применении функций f и g. На каждом шаге итерации для функции f вычисляется значение
где q - число
элементов ядра Аj, а для функции g – значение

где
Nj
- число элементов класса Рj.
Можно показать, что на практике алгоритм динамических
ядер уменьшает величину w,
определяемую на каждом шаге итерации. В реальных
применениях в процессе стремления к глобальному минимуму
могут встречаться локальные минимумы, вызванные либо усечением результатов численных расчетов, либо неудачным выбором
ядер.
Как уже упоминалось, один из возможных вариантов
нахождения ядер состоит в определении центра
тяжести каждого класса, т.е. каждое ядро состоит из
единственного элемента, являющегося центром тяжести соответствующего
класса. Некоторые авторы /365/ полагают,
что первым предложил процедуру итеративного
уточнения местоположения центров тяжести Торндайк
/353/, а затем она была усовершенствована в работах/292,338/.
Этот подход является очень
распространенным. Он лежит, например, в основе
предложенного Боллом и Холлом /257,258/ очень популярного в США
алгоритма, названного ISODАТА (итеративная самоорганизующаяся
система анализа данных). Алгоритм базируется на случайном отборе
k элементов в
качестве центров классов и в отнесении (без изменения центров классов) п-k оставшихся объектов к этим классам по принципу ближайшего соседства к
центру. После такого определения центры классов
пересчитываются. Если окажется) что два центра слишком близки друг
к другу, то два соответствующих класса) 6ъединяются; одновременно, если дисперсия одного класса
слишком клика, тогда он разделяется на два класса.
Этот процесс продолжается стабилизации центров классов и требует априорного
выбора “порогов", пороговых значений, в
сравнении со значениями которых принимается решение
о слиянии или разделении классов. При этом ровные
элементы классификации вырабатываются непосредственно в процессе работы. В
частности, это относится к числу классов, количество которых априори может быть не определено.
Известны некоторые
модификации алгоритма ISОDАТА, о6еспечивающие, например, его локальную оптимальность с помощью дополнительного многоточечного перераспределения /298/. В /339/ выводятся необходимые
и достаточные условия
получения специфических конфигураций
кластеров при работе алгоритма.
Важным
достоинством алгоритма является
возможность обработки больших массивов исходных данных (порядка десятка
тысяч), благодаря чему область применения этого алгоритма не ограничивается только распознаванием образов. Однако, основанный на минимизации критерия
квадратичного типа tг W, где W - объединенная внутригрупповая ковариационная матрица, алгоритм “чувствителен" к элементам,
слишком удаленным от центра тяжести классов.
Методы поиска модальных значений плотности
рассматривают кластер как область пространства с высокой плотностью точек по
сравнению с окружающими областями. Они "обследуют" пространство в
поисках скоплений в данных, которые и представляют собой области высокой плотности.
Существуют два основных вида методов поиска модальных значений плотности:
методы, основанные на кластеризации по одиночной связи,
и методы разделения смесей многомерных вероятностных
распределений.
Для проверки и сравнения различных методов кластерного
анализа предложен, например, пакет CLUSTER /328/. В /254,330/ описаны разработанные ЭС для выбора
процедуры кластеризации, соответствующей поставленным
условиям.
В настоящей работе автоматическая классификация данных
наполнена с помощью алгоритмов ISODАТА и
"ближайшего соседа". Преимущества этих алгоритмов, обусловившие их выбор,
указаны выше. результаты классификации используются для выбора возможного способа
повышения корреляций между физиологическими параметрами группах или популяциях. Рассматриваются два таких способа:
1) облако точек - объектов, представляющих группу в
пространстве параметров, более или менее равномерно вытягивается в небольшом
числе направлений;
2) это облако распадается на кластеры
(минимум - два), отстоящие друг от друга
на значительном расстоянии. В этом случае кластерам могут соответствовать
различные типы реакции объектов на адаптационную
нагрузку.
4.3.2. Результаты анализа
экспериментальных данных.
Из имеющегося объема данных были сформированы выборки,
на которых наблюдается
эффект группового стресса. Выборки составлялись в зависимости от
сезона года и
стадии нагрузки (при глюкозотолерантной нагрузке у детей пришлого
населения Таймыра с различной степенью конституционально-экзогенного ожирения и нормальным весом). Для зимы это группы с 1-ой (56 чел.), 2-ой (59 чел.), 2-ой
(57чел.) стадиями нагрузки; для весны - с
1-ой (45 чел.),
2-ой (45 чел.),
З-ей (49
чел.) стадиями; для лета - с 1-ой (53 чел.), 2-ой (51 чел.), 3-и (23 чел.), 4-ой (44 чел.) стадиями. Использовались, как наиболее информативные, показатели состояния липидного обмена плазмы крови: свободный холестерин (СХ),
свободные жирные кислоты (СЖК), триглицериды (ТГ),
эфиры холестерина (ЭХС), лизофосфатидилхохин ПФХ), сфингомиелин +
фосфатидилсерин (СМ+ФС),
фосфатидилхолин ФХ), фосфатидилэтаноламин (ФЭА). Данные были предоставлены сотрудниками НИИ медицинских проблем Севера СО РАМН (г.Красноярск).
Также были использованы данные, предоставленные
сотрудниками Российского университета Дружбы Народов (г. Москва). Контингент обследуемых -
практически здоровые люди, иностранцы, прибывшие для
обучения в Москву. Выборки составлялись с учетом региона постоянного проживания по 5-ти
состояниям срочной адаптации к гипоксии-гиперкапнии
(первое состояние - фоновое). На
основании этого обследуемые были объединены в группы: Латинская Америка, осень - по 17
человек на 4-х стадиях нагрузки и в фоновом состоянии; Юго-Восточная Азия,
осень - по
20 человек; Латинская Америка +
Юго-восточная Азия, осень - по 37 человек; то же для
зимы - по
24 человека. рассматривались показатели гемодинамики
и газообмена: общее .периферическое сопротивление (ОПС); систолическое давление (АДС);
диастолическое давление (АДД);
частота сердечных сокращений (ЧСС); ударный объем (УО); максимальный объем дыхания (МОД); количество выдыхаемого углекислого газа (СО2).
Автоматическая классификация данных проводилась на
основе алгоритма ISODАТА ("Итеративная самоорганизующаяся система анализа
данных") /223/ и с использованием
кластер - процедур ППП STATGRAPHICS, в частности, алгоритма "ближайшего соседа" (''single
linkage
or
nearest
neighbor"). Алгоритм ISODАТА реализован
в виде программы Gloud. За меру
близости между точками (объектами)
принималось евклидово расстояние.
Все данные предварительно нормировались (делились на среднеквадратическое отклонение), в качестве критерия
качества разбиения рассматривался функционал вида:
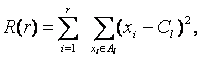
где r - число классов (групп), Сl - центр тяжести точек из класса Аl , Аl – l-й класс.
После проведенной в восьмимерном (глюкозотолерантная грузка) и семимерном (гипоксия - гиперкапния)
пространстве .осматриваемых параметров
классификации на два кластера в каждой рассматриваемых групп отсеялась часть
точек - объектов, не единенных в кластеры. В дальнейшем эти точки не
учитывались, т.е. объем анализируемых данных
составлял от 80% до 90% исходного при работе с алгоритмом ISODAТА и в среднем 60% при
использовании алгоритма "ближайшего
соседа". Количество точек в кластерах было в большинстве
случаев разным.
Сравнение расстояний (автоматическая классификация на
основе алгоритма ISODАТА) между центрами тяжести кластеров (S12) со одними расстояниями в них (S1 и S2) показало,
что кластеры в обоих случаях не являются
изолированными (таблицы 4.5, 4.6, 4.7).
Таблица 4.5. Внутрикластерные и межкластерные
расстояния в пространстве показателей липидного
обмена плазмы крови
Стадии |
зима |
весна |
лето |
||||||
|
нагрузки |
S1 |
S2 |
S12 |
S1 |
S2 |
S12 |
S1 |
S2 |
S12 |
|
I |
16,09 |
17,89 |
19,92 |
10,87 |
15,92 |
20,37 |
17.34 |
17.75 |
19,73 |
|
II |
17.02 |
21,51 |
24,52 |
13,24 |
16,85 |
19,45 |
17.59 |
14,67 |
18,81 |
|
III |
- |
- |
- |
11.03 |
15,50 |
21,08 |
10.32 |
12,51 |
15,61 |
|
IV |
13,54 |
20,59 |
22,72 |
- |
- |
- |
16,01 |
16,43 |
19,91 |
Из таблиц 4.6 и 4.7 видно, что при сравнительно небольшом объеме наблюдений (объектов), имевшемся в этом случае,
возможен вариант, когда межкластерное
расстояние S12 даже меньше средних расстояний
между точками в кластере 1(S1) и в кластере 2 (S2).
Таблица 4.6.
Внутрикластерные и межкластерные расстояния в пространстве
показателей гемодинамики и газообмена (региональные группы)
Стадии
|
Латинская Америка, осень |
Юго-Восточная Азия, осень |
||||
|
нагрузки |
S1 |
S2 |
S12 |
S1 |
S2 |
S12 |
|
I |
9.99 |
8,84 |
10.53 |
8,01 |
17,26 |
7,92 |
|
II |
12.78 |
10,73 |
7.87 |
12,16 |
12,36 |
11,17 |
|
III |
14,73 |
13,34 |
7.68 |
11,97 |
14,92 |
11.58 |
|
IV |
9.65 |
12,30 |
11,05 |
17.01 |
8,66 |
10.35 |
|
V |
10.49 |
9,57 |
10,72 |
13.15 |
13,42 |
10,96 |
Таблица 4.7.
Внутрикластерные и межкластерные расстояния в пространстве
показателей гемодинамики и газообмена (сезонные группы)
|
Стадии
нагрузки |
Осень,
Юго-Восточная Азия и Латинская Америка |
Зима,
Юго-Восточная Азия и Латинская Америка |
||||
|
|
S1 |
S2 |
S12 |
S1 |
S2 |
S12 |
|
I |
15.06 |
15,04 |
13,21 |
12,36 |
12,04 |
11.35 |
|
II |
19,42 |
15,10 |
8,91 |
15,17 |
11,57 |
12.96 |
|
III |
18.32 |
18,96 |
15.34 |
16.38 |
12,14 |
11.41 |
|
IV |
16.29 |
20,29 |
17.47 |
15.86 |
14,95 |
11.85 |
|
V |
18,57 |
17,13 |
13,21 |
13.69 |
13.17 |
13.40 |
Как показывает более детальное рассмотрение и
наглядное представление результатов классификации,
выделение кластеров в значительной степени
напоминает разрезание облака
точек перпендикулярно главной полуоси на две
группы. Чтобы получить возможность
наглядной интерпретации результатов классификации, были выполнены проекции порченных разбиений на
плоскости, соответствующие различным парам
параметров. Для каждой
группы было сделано, таким образом, по 28 проекций в случае глюкозотолерантной нагрузки и по 21- при нагрузке углекислым газом.
На рис. 4.1 представлены варианты наиболее
типичных проекций (алгоритм ISODATА), откуда видно, что сходная
группа в большинстве случаев, действительно, не распадается а изолированные
кластеры, а представляет собой некое достаточно компактное
облако.
Заметно также, что в
процессе увеличения нагрузки происходит смещение всей группы точек в
направлении, связанном с параметрами,
наиболее чувствительными к данному виду нагрузки. В рассматриваемом
случае – СО2 (Рис. 4.1.)
Сравнение
результатов классификации, полученных
с пользованием
разных алгоритмов, позволяет отметить как
их сходство, так и отличия. Заметно, например, что при внешнем сходстве полученных кластеров число учтенных, т.е.
попавших в кластеры точек,
больше в случае использования алгоритма ISODATA. Кроме того, для некоторых из
анализируемых групп данных глюкозотолерантная нагрузка - весна, лето, 2-я стадия; нагрузка углекислым
газом - Латинская Америка, осень, 3-я
стадия; Юго-Восточная Азия, осень, 3-я и 4-я
стадии; смешанная группа, зима, 4-я стадия)
классификация на два кластера с использованием алгоритма ближайшего соседа" оказалась неэффективной (число
точек в одном из кластеров было меньше 4-х, в силу
чего такой результат не учитывался).
Вышесказанное позволяет в конкретном случае выбирать
для классификации один из описанных алгоритмов,
исходя из практической целесообразности.
Сравнение полученных кластеров с
исходными группами по степени скоррелированности физиологических показателей
позволяет метить, что кластеры и исходные группы
различаются между собой рис. 4.2, 4.3).
Несмотря на то, что в случае нагрузки углекислым газом
исходные группы состоят из одних и тех же объектов,
полученные на каждом этапе кластеры отличаются по
составу. Это может говорить о том, что полированных
кластеров в изучаемом процессе действительно не возникает.
И, тем не менее, для интерпретации результата классификации можно проследить
формирование корреляционных взаимосвязей в зависимости
от стадии нагрузки в кластерах, выделенных на четвертой, максимальной, стадии нагрузки. Здесь мы исходим из
естественного предположения о том, что проявление
эффекта кластеризации, если он все-таки имеет
место, должно быть наиболее заметно именно при максимальной адаптационной
нагрузке.
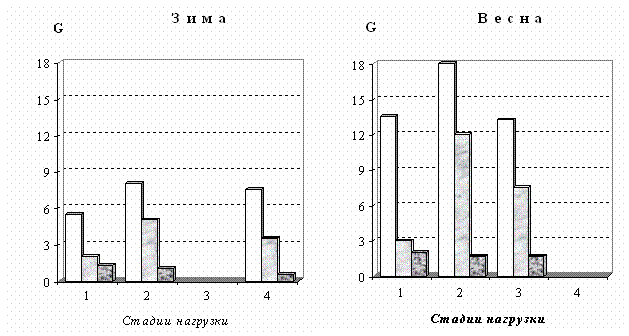
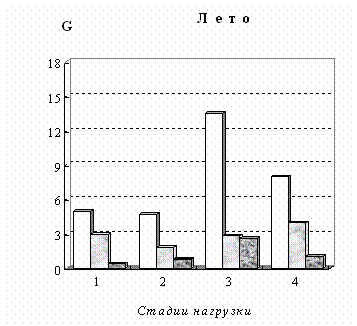
Действительно, из рис. 4.1. видно, что группы объектов, отнесенные на
четвертой стадии нагрузки к разным кластерам, на остальных стадиях имеют
сходную динамику веса корреляционного графа G. Особенно это заметно для групп
в которых численность объектов достаточно велика, чтобы делать статистически
более обоснованные выводы (юго-восточная Азия + Латинская Америка, осень). В
этих группах в обоих кластерах наблюдается отчетливый максимум степени скоррелированности показателей на первой стадии нагрузки,
что соответствует первому 2-хминутному состоянию с повышенным содержанием СО2 во
вдыхаемом воздухе. При этом кластеры отличаются друг от друга по значению G на этой стадии нагрузки.
Наличие
максимума напряжения на первой стадии нагрузки можно, по всей видимости,
объяснить мобилизацией компенсаторных механизмов,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Рис. 4.2. Степень скоррелированности показателей липидного обмена (алгоритм ISODATA) в исходной группе обследованных (
), после классификации в кластере 1 ( ) и в кластере 2 ( ).
Рис. 4.2. Степень скоррелированности показателей липидного обмена (алгоритм ISODATA) в исходной группе обследованных (
), после классификации в кластере 1 ( ) и в кластере 2 ( ).
![]()
![]()
![]()
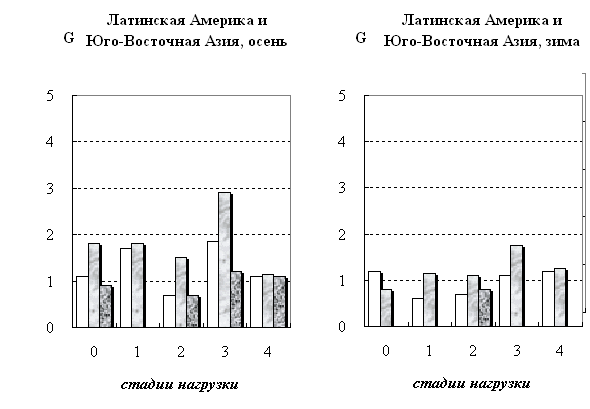
Рис.4.3. Степень скоррелированности
показателей гемодинамики и газообмена в
исходной группе обследованных (
), после классификации в кластере
1 ( ) и в кластере 2 ( ).
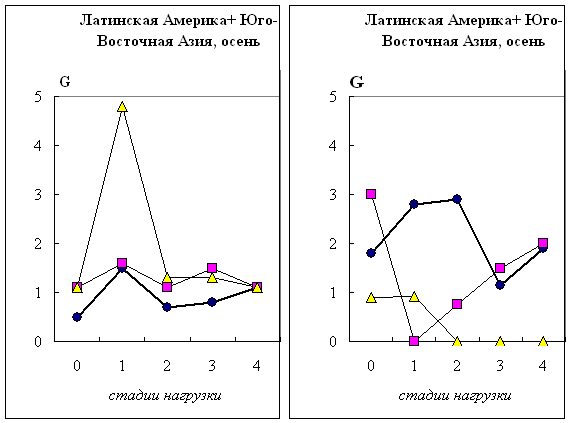
Рис. 4.4.
Изменение степени скоррелированности
показателей гемодинамики и газообмена в кластерах, выделенных на четвертой
стадии нагрузки
![]()
![]()
![]()
![]()
![]()
![]() исходная группа, кластер 1, кластер 2
исходная группа, кластер 1, кластер 2
обеспечивающих удовлетворительную
работу функциональных систем организма в ответ на адаптационную нагрузку.
Кластеры
могут быть также различным образом ориентированы в факторном пространстве
относительно друг друга и относительно целой группы
точек частями которой они являются. Здесь
возможны несколько вариантов: главные оси соответствующих эллипсоидов
параллельны или расположены под малыми углами друг к другу; главные оси одного
из эллипсоидов расположены под значительным углом к главным осям основного
эллипсоида; у обоих эллипсоидов рассеивания, соответствующих кластерам, главные
оси направлены под значительным углом друг к другу и к направлениям главных
осей эллипсоида целой группы и т.д.
Для
определения пространственной ориентации эллипсоидов рассеивания достаточно
найти углы между первыми собственными векторами соответствующих корреляционных
матриц (таблицы 4.8. – 4.10.).
Таблица 4.8.
Углы
между главными осями эллипсоидов рассеивания в пространстве показателей
липидного обмена, задаваемыми направлением первых собственных векторов, и соответствующими исходной группе (А), а также разным кластерам (В,С)
|
Стадии
нагрузки |
зима |
весна |
Лето |
||||||
|
jАВ, ° |
jАС, ° |
jВС, ° |
jАВ, ° |
jАС, ° |
jВС, ° |
jАВ, ° |
jАС, ° |
jВС, ° |
|
I
|
22.90 |
78.03 |
64.79 |
46.8 |
9.94 |
51.61 |
73.82 |
20.49 |
68.73 |
|
II |
0.95 |
32.54 |
12.98 |
4.17 |
19.94 |
23.88 |
22.44 |
27.18 |
43.15 |
|
III |
- |
- |
- |
25.57 |
20.28 |
37.49 |
17.04 |
40.63 |
53.95 |
|
IV |
49.53 |
31.02 |
73.81 |
- |
- |
- |
19.32 |
74.30 |
74.25 |
Из анализа таблиц вино, что имеет
место случай, когда ориентация обоих кластеров относительно целой группы
различна. Причем, как правило, угол между главными осями кластеров (j ВС) ) больше, чем углы отклонения одного из кластеров от главной оси эллипсоида целой группы.
Таблица 4.9.
Углы
между главными осями эллипсоидов рассеивания в пространстве показателей
гемодинамики и газообмена, задаваемыми направлением первых собственных
векторов, и соответствующими исходной
группе (А), а также разным кластерам (В,С)
|
Стадии
нагрузки |
Латинская Америка, осень |
Юго-Восточная
Азия, осень |
|||||
|
jАВ, ° |
jАС, ° |
jВС, ° |
jАВ, ° |
jАС, ° |
jВС, ° |
||
I
|
39,35 |
48,02 |
74,30 |
30,51 |
47,94 |
75,84 |
|
|
II |
34,31 |
78,04 |
75,08 |
24,94 |
54,86 |
62,04 |
|
|
III |
78,65 |
40,37 |
85,57 |
44,95 |
24,35 |
58,86 |
|
|
IV |
40,68 |
42,91 |
75,53 |
45,70 |
56,23 |
85,91 |
|
|
V |
88,86 |
89,78 |
63,84 |
86,34 |
70,31 |
88,73 |
|
Таблица 4.10.
Углы
между главными осями эллипсоидов рассеивания в пространстве показателей
гемодинамики и газообмена, задаваемыми направлением первых собственных
векторов, и соответствующими исходной
группе (А), а также разным кластерам (В,С)
|
Стадии нагрузки |
Латинская
Америка и Юго-Восточная Азия, осень |
Латинская
Америка и Юго-Восточная Азия, зима |
|||||
|
jАВ, ° |
jАС, ° |
jВС, ° |
jАВ, ° |
jАС, ° |
jВС, ° |
||
I
|
47,25 |
22,34 |
66,82 |
89,92 |
16,89 |
84,55 |
|
|
II |
44,94 |
23,07 |
65,76 |
31,45 |
20,28 |
50,36 |
|
|
III |
65,24 |
38,19 |
83,23 |
34,24 |
76,36 |
56,17 |
|
|
IV |
39,95 |
27,69 |
54,05 |
14,00 |
34,56 |
47,32 |
|
|
V |
35,78 |
40,75 |
36,95 |
60,33 |
51,19 |
38,55 |
|
Проверка достоверности кластерного решения,
выполненного с помощью алгоритма ISODАТА для
рассматриваемого критерия качества разбиения,
проводилась согласно /113/ по тесту
значимости для внешних признаков. Согласно этому тесту полученные в случае глюкозотолерантной нагрузки кластеры сопоставлялись
по 10
признакам (с их градациями), не участвовавшим при
формировании (кластеров: 1.
пол (мужской, женский), 2. длительность
болезни (до 3-х т; 3-5 лет; свыше 5 лет), 3.
длительность проживания на Севере (1-3 “да; 3-5 лет; более
5 лет; с рождения), 4. наличие
наследственной предрасположенности к заболеванию
(да; нет), 5.
характер вскармливания до года (естественное;
искусственное; смешанное), преобладающий характер питания матери во время
беременности елки; жиры; углеводы; смешанное), 7. соответствие полового развития трасту (соответствует; отстает; ускоренное), 8. наличие осложнений со стороны сердечно-сосудистой системы (есть; нет), 9. фаза ожирения простая;
переходная; осложненная), 10. степень ожирения (нормальный с; 1-я; 2-я; 3-я).
В результате сравнения кластеров (рис. 4.5, 4.6) видно, что значимых
и повторяющихся различий между ними по независимым признакам
нет, т.е. кластеры практически неразличимы. Это подтверждает
результат классификации о том, что кластеры не удалены 1 значительное расстояние друг от друга
в пространстве показателей липидного обмена.
Таким образом, в описанных случаях
наиболее типичным особом повышение корреляций в группе (популяции) происходит не за счет
распада ее на изолированные кластеры и их расхождения в пространстве параметров (что
могло бы говорить о существовании яличных типов реакции на адаптационную нагрузку).
Выборка остается однородной.
Полученный результат позволяет
высказать гипотезу о том, что эффект повышения
корреляций при увеличении адаптационного напряжения не связан с образованием изолированных подгрупп,
а связан увеличением относительного вклада
некоторых факторов, за счет чего облако данных вытягивается в пространстве
анализируемых параметров;
небольшом числе направлений.
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
10.В |
|
|
|
|
|
|
10.В |
|
|
|
|
|
|
|
10.В |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
10.А |
|
|
|
|
|
|
10.А |
|
|
|
|
|
10.А |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
9.В |
|
|
|
9.В |
|
|
|
|
|
|
|
9.В |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
9.А |
|
|
|
|
|
|
|
9.А |
|
|
|
9.А |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
8.В |
|
|
|
8.В |
|
|
|
|
|
|
|
|
8.В |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
8.А |
|
|
|
|
|
|
|
8.А |
|
|
|
8.А |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
7.В |
|
|
|
|
|
|
|
7.В |
|
|
|
|
|
|
7.В |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
7.А |
|
|
|
|
|
|
|
|
|
|
|
7.А |
|
|
|
|
|
7.А |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
6.В |
|
|
|
|
|
|
|
6.В |
|
|
|
|
|
|
6.В |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
6.А |
|
|
|
|
|
|
|
|
6.А |
|
|
|
|
|
|
6.А |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
5.В |
|
|
|
|
|
|
|
|
5.В |
|
|
|
|
|
|
|
5.В |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
5.А |
|
|
|
|
|
|
|
|
5.А |
|
|
|
|
|
|
|
|
|
5.А |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
4.В |
|
|
|
|
|
|
|
4.В |
|
|
|
|
|
4.В |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
4.А |
|
|
|
|
|
|
4.А |
|
|
|
|
|
|
|
|
|
|
4.А |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
3.В |
|
|
|
3.В |
|
|
|
3.В |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
3.А |
|
|
|
|
|
|
|
3.А |
|
|
|
3.А |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2.В |
|
|
|
|
|
|
2.В |
|
|
|
|
|
|
2.В |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2.А |
|
|
|
|
|
|
2.А |
|
|
|
|
|
|
2.А |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1.В |
|
|
|
|
|
|
1.В |
|
|
|
|
1.В |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1.А |
|
|
|
|
|
1.А |
|
|
|
|
1.А |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Глюкозотолерантный тест, зима
Рис. 4.5. Сравнение
кластеров (А,В) по тесту значимости для внешних
признаков (1-10). Градации признака даны в процентном отношении.
|
10.В |
|
|
|
|
10.В |
|
|
|
|
10.В |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
10.А |
|
|
|
|
10.А |
|
|
|
|
10.А |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
9.В |
|
|
9.В |
|
|
|
9.В |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
9.А |
|
|
9.А |
|
|
|
9.А |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
8.В |
|
|
8.В |
|
|
|
8.В |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
8.А |
|
|
|
8.А |
|
|
|
8.А |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
7.В |
|
|
|
|
7.В |
|
|
|
7.В |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
7.А |
|
|
|
|
7.А |
|
|
|
|
7.А |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
6.В |
|
|
|
|
|
6.В |
|
|
|
|
6.В |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
6.А |
|
|
|
6.А |
|
|
|
|
6.А |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
5.В |
|
|
|
|
5.В |
|
|
|
|
5.В |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
5.А |
|
|
|
|
5.А |
|
|
|
|
5.А |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
4.В |
|
|
|
4.В |
|
|
4.В |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
4.А |
|
|
|
4.А |
|
|
4.А |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
3.В |
|
|
|
|
3.В |
|
|
|
|
|
3.В |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
3.А |
|
|
|
|
3.А |
|
|
|
|
3.А |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2.В |
|
|
|
|
2.В |
|
|
|
2.В |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2.А |
|
|
|
|
2.А |
|
|
|
|
2.А |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1.В |
|
|
|
1.В |
|
|
|
1.В |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1.А |
|
|
|
1.А |
|
|
|
1.А |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0% |
50%
100% нагрузка 1 |
|
0% |
50% 100% нагрузка 2 |
|
0% |
50% 100% нагрузка
3 |
||||||||
Глюкозотолерантный тест, зима
Рис. 4.6.
Сравнение кластеров (А,В) по тесту значимости для
внешних признаков (1-10).
Таким образом, выполнена автоматическая классификация
имеющихся данных, проведена проверка кластерного решения. Полученные результат
дают снования утверждать, что
• во всех рассмотренных случаях увеличение корреляций
при усилении адаптационной нагрузки происходит не путем кластеризации, а за
счет выделения некоторого числа факторов, определяющих в пространстве состояний
направления преимущественного растяжения облака данных;
• гипотеза о том, что повышение корреляций не связано
с кластеризацией (кластеры могли бы соответствовать различным типам
реакции на адаптационную нагрузку),
не противоречит
экспериментальным данным.
4.4. Определение точек максимальной интеграции подсистем, обеспечивающих физическую работоспособности при нагрузочных тестах
В
данном разделе с помощью модификации метода корреляционной адаптометрии
предложен способ количественной оценки интеграции подсистем функциональной
системы, обеспечивающей физическую работоспособность. Выявлены точки
максимальной интеграции подсистем при физической нагрузке. Разработан алгоритм
для определения степени интеграции k
подсистем на m этапах нагрузочных тестов.
4.4.1. Интеграция
функциональных систем организма
Организм человека представляет собой сложную гармоничную систему,
поддерживающую гомеостаз на всех уровнях своей организации. Мультипараметрический
принцип взаимодействия различных функциональных систем
определяет их обобщенную деятельность. Однако в различных условиях и под
действием различных факторов расход ресурсов функциональных систем на поддержание системы в некотором устойчивом состоянии
неодинаков /142,215/.
Как правило, изменение одного
показателя, результата деятельности одной функциональной системы немедленно
сказывается на результатах деятельности других
функциональных систем /215/.
В целом в организме каждая
функциональная система, стремясь обеспечить
прежде всего свой результат, влияет на деятельность других функциональных систем, при этом вносит
соответствующие возмущения в процессы их саморегуляции.
Конечный результат деятельности взаимосвязанных функциональных систем
существенно отличается от тех результатов, которые имели бы отдельные
функциональные системы, действуя порознь.
Функциональная
система может быть представлена как совокупность взаимодействующих подсистем. В
данном разделе предложен способ оценки степени интеграции
параметров подсистем гемодинамики и газообмена при нагрузочных
тестах. Нами была выдвинута гипотеза о
том, что уровень интеграции подсистем функциональной системы зависит от
величины внешних воздействий – этапа нагрузки, состояния организма и степени
адаптационного напряжения. В качестве результата деятельности подсистем
гемодинамики и газообмена при нагрузочных тестах рассматривался уровень
физической работоспособности.
Для
получения количественной оценки степени интеграции подсистем функциональной
системы, обеспечивающей физическую работоспособность, был привлечен метод
главных компонент. Данные, с которыми мы имели дело, измерялись непосредственно
в ходе нагрузочной пробы и в период восстановления.
В
качестве примера определения точек наибольшей интеграции
подсистем функциональной системы, обеспечивающей физическую
работоспособность, рассмотрим данные группы мужчин 20-29 лет в различные
периоды года. В первой строке – значения компоненты для состояния покоя, далее
– по этапам нагрузки
4.4.2.
Определение точек максимальной интеграции подсистем, обеспечивающих физическую
работоспособность, при нагрузочных тестах
Исследуемый объект или явление
характеризуется множеством признаков, измеряемых непосредственно. Однако
внутреннюю структуру явления характеризуют не сами признаки, а внутренние
факторы, свойства, присущие этой совокупности объектов, которые не всегда
поддаются непосредственному измерению. Один из способов выявления таких
факторов - метод главных компонент. Главные компоненты определяют факторную
структуру явления, которая характеризуется с помощью коэффициентов корреляции
между признаками и главными компонентами.
Анализ факторной структуры позволяет
выявить скрытые, но объективно существующие закономерности, описывающие
внутренние факторы и определяющие состояние исследуемой системы , позволяет также выявить признаки, наиболее тесно
связанные с данными факторами, что позволяет про анализировать функционирующую
систему,
Каждый внутренний фактор также может быть представлен
в виде функции от наблюдаемых признаков. Таким образом, мы можем перейти к
новым интегральным количественным показателям того или иного обобщающего
свойства, заключенного в данном факторе. При этом функциональная система может
быть представлена как совокупность взаимодействующих подсистем.
Априори известно, что в 1-ю подсистему
входят признаки с номерами i =1, …, n1 во 2-ю подсистему - с номерами i =n1 + 1, …, n2, в k-ю подсистему входят признаки с
номерами i =nk-1 + 1, …, nk, причем nk = т.
Выдвигается гипотеза о том, что уровень
интеграции подсистем функциональной системы зависит от величины внешних
воздействий (этапа нагрузки, состояния организма и адаптационного фона).
Наша задача - построить количественный
критерий измерения уровня интеграции подсистем, с помощью этого критерия
исследовать работу подсистем, участвующих в обеспечении целевого показателя (в
нашем случае - в обеспечении физической работоспособности), при нагрузочных
тестах. Нами предлагается алгоритм, иллюстрирующий последовательность
построения такого критерия (рис. 4.7.).
Основной задачей расчетных процедур при
определении точек максимальной интеграции подсистем в пространстве:
коэффициент корреляции -этап нагрузки - является
получение матрицы А. Исходными
данными для расчетов служит
матрица X, т.е. совокупность всех
измеряемых признаков (параметров) у всех объектов. В этой матрице каждый
элемент хij
обозначает значение j-го
признака у i-го объекта.
На первом этапе элементы матрицы X преобразуют в элементы матрицы Z={zij}, которые получаются с помощью нормирования и центрирования матрицы X:
![]()
где ![]() - математическое
ожидание значений j-го признака, sj – среднее квадратическое
отклонение этих значений. На втором этапе обработки с помощью матрицы Z определяем корреляционную матрицу R , т.е. совокупность коэффициентов парной
корреляции изучаемых признаков. Затем оцениваем вес корреляционного графа G.
- математическое
ожидание значений j-го признака, sj – среднее квадратическое
отклонение этих значений. На втором этапе обработки с помощью матрицы Z определяем корреляционную матрицу R , т.е. совокупность коэффициентов парной
корреляции изучаемых признаков. Затем оцениваем вес корреляционного графа G.
На третьем этапе определяем матрицу А - матрицу коэффициентов корреляции
главных компонент с измеряемыми признаками.
На четвертом этапе обработки по элементам {аij} находим нормированное значение
степени интеграции для каждой исследуемой подсистемы. Для этого сумму
коэффициентов корреляции главных компонент с признаками каждой подсистемы делим
на количество признаков полсистемы. Определяем точки максимальной интеграции.
Алгоритм определения точек интеграции параметров подсистем при
нагрузочных тестах
Этапы обработки
|
|
Матрицы |
Содержание матриц
|
|
|
|
|
|
|
|
|
I…j…m |
|
|
|
I |
X = {xij} |
Матрица
исходных данных, j
– номер признака i-го объекта |
|
i |
|||
|
N |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
I…j…m |
|
|
|
I |
Z = {zij} |
Преобразованная
матрица |
|
|
i |
||
|
|
N |
||
|
|
|
|
|
|
|
|
|
|
|
|
I…j…m |
|
|
|
|
I |
R = {rij} |
Корреляционная
матрица |
|
|
l |
||
|
|
m |
||
|
|
|
|
|
|
|
I…j…m |
|
|
|
|
I |
A = {aij} |
Матрица
коэф-тов кор-реляции ГК с
признака-ми: k - номер главной компоненты, j - номер признака
l - число ГК |
|
|
k |
||
|
|
l |
||
|
|
|
|
|
|
Определение точек макси-мальной интеграции отдельных подсистем на
каждом этапе нагрузки |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
U11 – для подсистемы
гемодинамики. U12 - для подсистемы
дыхания |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис.
4.7. Последовательность расчетов при нахождении
точек интеграции подсистем при нагрузочных тестах. |
|||
Если первая главная компонента коррелирует с «т»
исследуемыми признаками «k» различных подсистем, то для i-этапа нагрузки имеет место соотношение
где ![]() - количество этапов нагрузки, пл, = т. Иначе, можно записать
- количество этапов нагрузки, пл, = т. Иначе, можно записать
Делим сумму модулей коэффициентов
корреляции аij, для каждой подсистемы на
количество n1 ,n2,,...,nk признаков соответственно.
Получаем совокупность значений {uip}, где i - номер этапа нагрузки, р- номер подсистемы ![]()
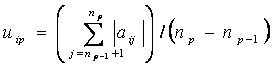 .
.
Определяем значение степени интеграции
каждой подсистемы для каждого этапа нагрузки. Завершающим этапом является
нахождение максимального значения иip в столбце матрицы.
Полученные максимальные значения показателей интеграции
подсистем позволяет выделить уровни воздействий, наиболее сильно влияющие на напряжение
функциональной системы.
В качестве иллюстрации
предложенного алгоритма определим точки наивысшей интеграции
подсистем функциональной системы обеспечения физической работоспособности
при нагрузочных тестах. Для этого рассмотрим связь первой главной компоненты с
признаками для состояния покоя и на разных этапах нагрузки для группы 20-29
лет в различные периоды года. Отметим лишь наиболее сильные
(>0.5) корреляционные связи (для каждого сезона в первой строке - значения
компоненты для состояния покоя, и далее - по этапам нагрузки, z1…z5 -нормированные
признаки подсистемы гемодинамики, z6…z8 - признаки подсистемы дыхания, уi - первая главная компонента, i - стадия нагрузки, опущены
и заменены «пробелами» признаки, не имеющие «сильной» связи с главным
фактором):
для периода вхождения в полярную ночь:
|
Y0 = |
0.78z1 |
|
+0.64 z3 |
|
-0.64 z5 |
+0.59 z6 |
-0.41 z7 |
-0.57 z8 |
|
Y1 = |
|
|
|
-0.52 z4 |
|
-0.79 z6 |
-0.88 z7 |
-0.91 z8 |
|
Y2 = |
0.82 z1 |
|
|
|
|
-0.72 z6 |
-0.78 z7 |
-0.74 z8 |
|
Y3 = |
0.84 z1 |
|
|
|
-0.83 z5 |
-0.52 z6 |
|
|
|
Y4 = |
0.76 z1 |
+0.52 z2 |
|
|
-0.77 z5 |
-0.79 z6 |
|
-0.71 z8 |
для периода полярной ночи:
|
Y0 = |
0.65z1 |
+0.55 |
+0.89 z3 |
+0.59 |
|
|
+0.55 z7 |
+0.59 z8 |
|
Y1 = |
|
|
|
|
|
+0.78 z6 |
+0.94 z7 |
+0.94 z8 |
|
Y2 = |
|
|
|
-0.65 z4 |
|
-0.75 z6 |
-0.93 z7 |
-0.94 z8 |
|
Y3 = |
0.80 z1 |
+0.92 |
+0.81 |
+0.92 z4 |
-0.96 z5 |
+0.96 z6 |
+0.91 z7 |
+0.91 z8 |
|
Y4 = |
0.74 z1 |
-0.67 z2 |
|
|
-0.6 z5 |
|
-0.81 z7 |
-0.78 z8 |
для периода выхода из полярной ночи:
|
Y0 = |
0.82z1 |
+0.66 z2 |
+0.57 z3 |
-0.52 z4 |
|
-0.53 z6 |
|
|
|
Y1 = |
0.57 z1 |
+0.7 z2 |
+0.84 z3 |
+0.88 z4 |
-0.95 z5 |
+0.79 z6 |
+0.92 z7 |
+0.94 z8 |
|
Y2 = |
0.63 z1 |
|
|
|
+0.81 z5 |
|
+0.75 z7 |
+0.79 z8 |
|
Y3 = |
|
|
|
|
+0.68 z5 |
+0.71 z6 |
+0.86 z7 |
+0.76 z8 |
|
Y4 = |
0.86 z1 |
|
|
|
-0.86 z5 |
|
-0.88 z7 |
-0.83 z8 |
для периода полярного дня:
|
Y0 = |
|
+0.72 z2 |
|
|
+0.51 z5 |
|
-0.86 z7 |
+0.87 z8 |
|
Y1 = |
0.88 z1 |
-0.61 z2 |
|
-0.86 z4 |
-0.63 z5 |
-0.66 z6 |
-0.77 z7 |
-0.78 z8 |
|
Y2 = |
0.92 z1 |
|
|
-0.82 z4 |
-0.59 z5 |
-0.81 z6 |
-0.87 z7 |
-0.96 z8 |
|
Y3 = |
0.83 z1 |
|
|
+0.71 z4 |
+0.72 z5 |
-0.78 z6 |
-0.75 z7 |
+0.93 z8 |
Следует отметить, что на всех этапах
нагрузки первая главная компонента имеет самые большие значения корреляций с
параметрами дыхания. Обращает на себя внимание тот факт, что сильные
корреляционные связи со всеми рассматриваемыми параметрами имеются на 3-м этапе
нагрузки в период полярной ночи, и на первом этапе - в период выхода из
полярной ночи.
При рассмотрении параметров гемодинамики в
различные периоды года группе 20-29 лет выявлено, что высокие значения
корреляции первой главной компоненты (ГК) с параметрами этой подсистемы в
период вхождения в полярную ночь достигается на 4-м этапе нагрузки, в период
полярной ночи -на 3-м этапе нагрузки, а в период
выхода из полярной ночи и в полярный день самая высокая интеграция достигается
уже на 1-м этапе. Максимум интеграции для этого
возраста приходится на 3-й этап в период полярной ночи и на 1-м -этапе - в период выхода из нее. (рис.4.8.).
При
проведении аналогичных исследований в группе 30-39 лет установлены сильные
корреляционные связи ГК с параметрами гемодинамики для периода вхождения в
полярную ночь - на 1-м и 4-м этапе, для полярной ночи - это 2-й этап, для
периода выхода из полярной ночи - в покое (до начала нагрузочных тестов) и на
2-м этапе (V- нет данных). Наивысшей точки
интеграция параметров подсистем достигает в период вхождения в полярную ночь на
4-м этапе.
При исследовании подсистемы гемодинамики для группы 40-49 лет I
наивысшая точка интеграции этой подсистемы прослеживается на 1-м этапе нагрузки .
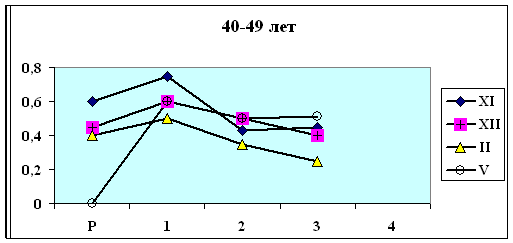
Рис.
4.8. Точки максимальной интеграции параметров подсистемы гемо-
динамики для разных возрастных
групп в состоянии покоя (Р) и на
этапах нагрузки (1-4) в периоды года: XI-вхождение в полярную ночь, XII-полярная
ночь, II-выход из полярной ночи, V-полярный день.
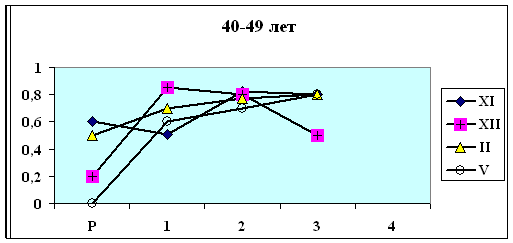
Рис.
4.9. Точки максимальной
интеграции параметров подсистемы дыхания для разных возрастных групп в состоянии
покоя (Р) и на этапах нагрузки (1-4) в периоды года:
XI-вхождение в полярную ночь, XII-полярная ночь, II-выход из полярной ночи,
V-полярный день.
Далее были исследована интеграция
параметров подсистемы дыхания (рис.4.9.). Для группы 20-29 лет выявлена
наибольшая зависимость ГК от этих параметров в период вхождения в полярную ночь
- на 2-м этапе, в период полярной ночи - на 1 и 3-м этапе, в период полярного
дня - на 2-м этапе. Максимум интеграции выявлен на 3-м этапе в период полярной
ночи.
В группе 30-39 лет при выполнении
нагрузочных тестов сильные корреляционные связи ГК с параметрами подсистемы
дыхания выявлены в следующие периоды и этапы: вхождение в полярную ночь - в
покое и на 1-м этапе- полярная ночь - в покое- выход
из полярной ночи - 1 и 3-й этап. Максимальная интеграция подсистем приходится
на 1-й этап в период выхода из полярной ночи.
В группе 40-49 лет точкой наивысшей
интеграции подсистем дыхания для периода вхождения в полярную ночь является 2-й
этап, для полярной ночи - 1-й этап, для выхода из полярной ночи - 2-й этап, а в
полярный день 3-й этап. Для этой группы исследуемых стоит
отметить резкое (по сравнению с состоянием покоя) увеличение корреляционной
зависимости ГК от параметров дыхания. Такая зависимость сохраняется и
на последующих этапах нагрузки.
В дальнейших исследованиях первой главной
компоненты корреляции параметров гемодинамики были сопоставлены с корреляциями
подсистемы дыхания (рис.4.10.).
Установлено, что в группе 20-29 лет в состоянии покоя
подсистемы гемодинамики и дыхания имеют небольшую разницу в корреляции с ГК.
Затем с возрастанием нагрузки в период выхода из полярной ночи и в полярный
день происходит синхронное возрастание этих значений на первом этапе нагрузки.
При дальнейшем увеличении нагрузки в период вхождения в полярную ночь
происходит некоторый спад интеграции подсистем, в полярную ночь наблюдается
противоположное поведение подсистем.
В целом можно сказать, что для
20-29-летнего возраста поведение подсистем гемодинамики и дыхания при
выполнении нагрузки имеет вид петли, на некоторых этапах прослеживается
противоположное поведение подсистем.
Рис. 4.10. Точки максимальной интеграции подсистем гемодинамики (НЕМ) и дыхания (О2) при нагрузочных тестах для группы мужчин 20-29 лет.
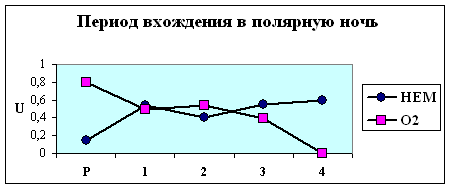
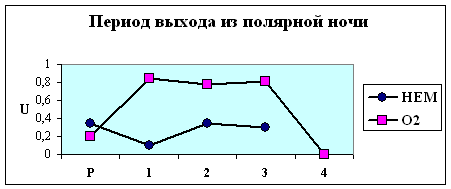
Рис. 4.11. Точки
максимальной интеграции подсистем гемодинамики (НЕМ) и дыхания
(О2)
при нагрузочных тестах
для группы мужчин 30-39
лет.
Можно предположить их компенсаторную
функцию друг для друга: с увеличением интеграции дыхания снижается величина
интеграции параметров гемодинамики и наоборот.
Для 30-39-летних (рис.4.11.) в период
вхождения в полярную ночь и в период полярной ночи в состоянии покоя характерна
большая разница в степени корреляции ГК с исследуемыми подсистемами: очень
высокая - для дыхания и очень низкая - для гемодинамики. На первом этапе наблюдается
сближение интеграции подсистем. Можно выделить этапы (1-3-й этап), когда
наблюдается небольшой диапазон изменения интеграции подсистемы дыхания и гемодинамики,
а затем снова расхождение. В целом, поведение подсистем при возрастании
нагрузки имеет форму "вилки'.
Для 40-49-летних характерны близкие
«стартовые» корреляции ГК с подсистемами (рис.4.12.). В период вхождения в
полярную ночь на 1-м этапе наблюдается противоположная реакция подсистем на
возрастание нагрузки.
В остальные периоды года на 1-м
этапе происходит синхронное увеличение интеграции подсистем, а при дальнейшем
увеличении нагрузки, на последующих этапах, также противоположная реакция на
нагрузку. Видимо, при увеличении нагрузки происходит саморегуляция
кардиореспираторной системы, ее перестройка, для
преодоления нагрузки.
На рис.4.13. представлена
результирующая картина по определению и интеграции подсистем функциональных
систем, обеспечивающих физическую работоспособность, при нагрузочных тестах
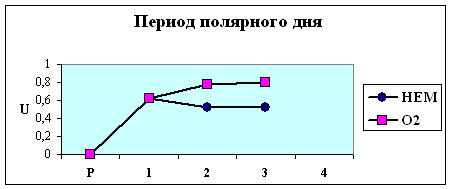
Рис.
4.12. Точки максимальной интеграции подсистем гемодинамики
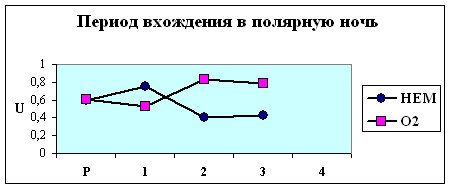
(НЕМ)
и дыхания (О2) при
нагрузочных тестах для
группы мужчин 40-49 лет.
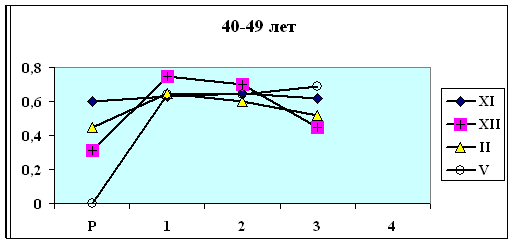
Рис. 4.13. Точки интеграции подсистем функциональной системы, обеспе- чивающей
физическую работоспособность при
нагрузочных тестах для разных
возрастных групп в состоянии покоя
(Р) и
на этапах нагрузки (1-4) в
периоды года: XI-вхождение в
полярную ночь, XII-полярная ночь, II-выход из полярной ночи, V-полярный
день.
Таким образом, выявлено существование точек максимальной
интеграции функциональных подсистем, обеспечивающих физическую
работоспособность. Установлено, что расположение этих точек
на шкале нагрузок и степень интеграции подсистем зависит от общего состояния
организма (возраст), ветчины нагрузки и климатического фона (период года): в
группе 20-29 лет максимум интеграции подсистем приходится в период полярной
ночи на 3-й этап нагрузки; для 30-39-летних он приходится на 1-й этап в период
выхода нз полярной ночи; в группе 40-49 лет
максимум интеграции исследуемых подсистем наблюдался в период полярного дня на
3-м этапе.
При выполнении нагрузочных тестов
при уменьшении интеграции подсистемы гемодинамики возрастает интеграция
подсистемы дыхания. У 20-29-летних проявляется тенденция к регуляции работы подсистем,
обеспечивающих физическую работоспособность, как реакция на возрастающую
нагрузку, У 30-39-летних такая тенденция более выражена. У 40-49-летних
компенсаторная роль подсистем прослеживается еще в большей степени.
Наблюдается более напряженная работа
(высокая степень интеграции) подсистемы дыхания во все периоды года особенно в
период полярной ночи и период полярного дня.
Таким образом, предложен способ
количественного измерения уровня интеграции подсистем
функциональной системы. Он может служить способом для выделения точек
максимальной интеграции функциональных систем при выполнении нагрузочных
тестов. Данный способ может быть полезен при выявлении наиболее значимой из
подсистем, входящих в единую интегрированную систему при внешнем воздействии и
интеграции этих подсистем.
ВЫВОДЫ
1. Сравнение популяций и
групп людей по числу действующих факторов может служить средством для изучения адаптированности. Основанный на этом подход назван нами
корреляционной адаптометрией.
2. Предложена система
математических моделей сдвига параметров в результате увеличения адаптационной
нагрузки.
3. Увеличение корреляций
при усилении адаптационной нагрузки происходит не за счет образования
кластеров, а за счет растяжения облака данных в пространстве состояний в
небольшом числе направлений.
4. Предложен способ
количественного измерения, представления интеграции подсистем функциональных
систем.